今回はE検定対策としてScikit-Learnのうち、分類モデルの代表的なK最近傍法(K-Nearest Neighbor) (以下k-NN法)について解説します。

分類モデルのうちk-NN法の概要が知りたい!
実際にk-NN法での機械学習モデルのプログラミング手法を知りたい!

本記事ではそんな疑問にお答えします。
K最近傍法(K-Nearest Neighbor)による分類 とは?
k-NNはもっとも単純な分類アルゴリズムであり、予測したいデータと距離の近いk個のモデルデータのラベルから予測値を決定するアルゴリズムです。
以下にk-NN法分類のメリット/デメリットをまとめます。
メリット
- モデルの過度な調整をせずにある程度の精度が出る
- アルゴリズムの理解が容易
デメリット
- データの前処理が必須
- 特徴量(数百以上)の多いデータセットではうまく機能しない
- 疎なデータセットでは精度が出ない
- 処理速度が遅い
上記のデメリットから実務上はあまり使われることはありませんが、E検定では出題されますので、分類の基礎知識として必須です。
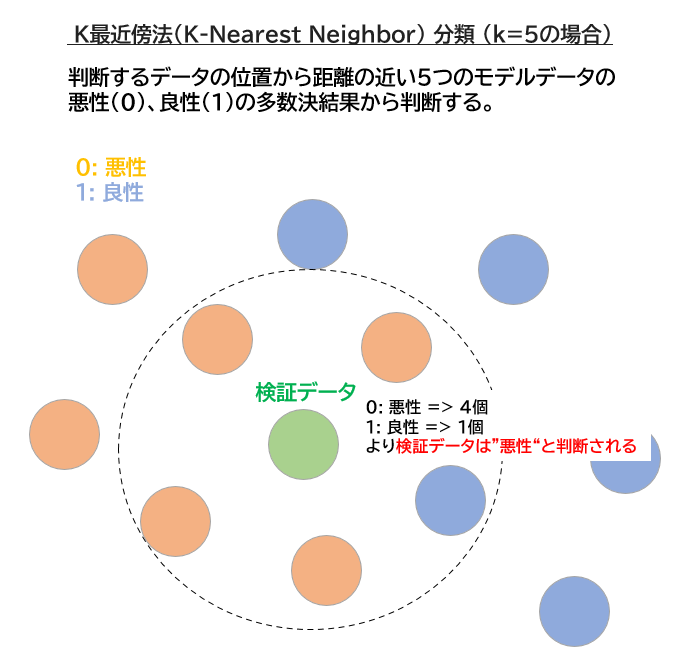

多数決をとる人数がk-NNのkなんだね!
k-NN Classifier パラメータの詳細
k-NN分類予測のためのハイパーパラメータには以下があります。
詳細は以下、Scikit-Learnの公式サイトより確認ください。
当たり前ですが最も重要なハイパーパラメータはアルゴリズム判断に用いる近傍点の数(n_neighbors)です。
今回のプログラムサンプルではこの近傍点の数を変数に予測精度を確認します。
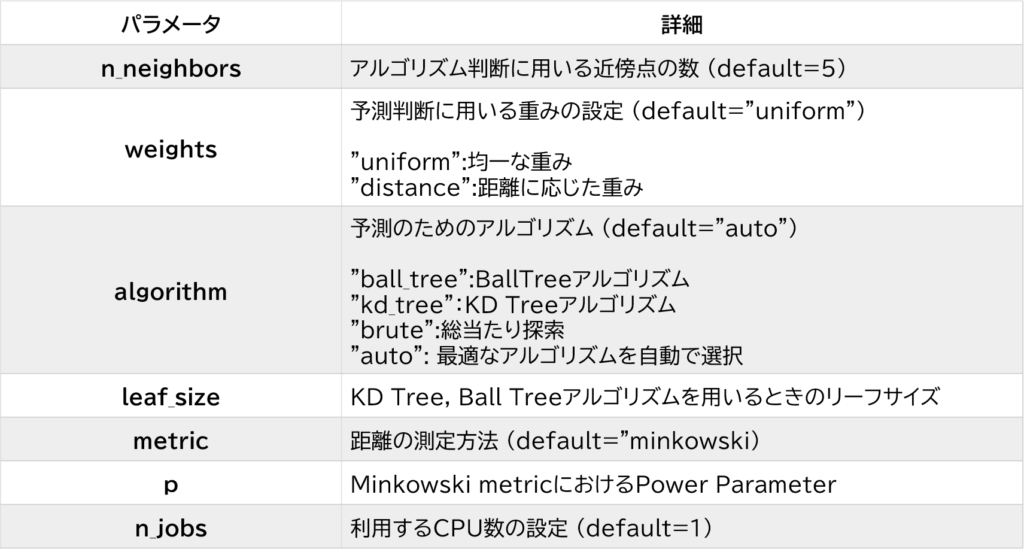
何も設定しなければ近傍点の数は5になるよ!

Scikit-Learn Cancer Datasetによる分類モデルの構築
必要なライブラリの読み込み
実際にScikit-LearnのCancer Datasetを用いて分類予測を行います。
まず機械学習予測に必要な必要なライブラリを読み込みます。 "classfication_report"は予測値の評価に用います。
# 必要なライブラリの読み込み
# Jupyter Notebook上にグラフを表記するために記載
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
# 訓練データ/教師データの分割用
from sklearn.model_selection import train_test_split
# 予測値の評価用
from sklearn.metrics import classification_report
#sklean cancer dataの読み込み
from sklearn.datasets import load_breast_cancerCancer Datasetの確認
分類のデータサンプルとしてScikit-Learnの提供する乳がんの分類データセットを使用します。
データセットの詳細はこちら↓
以下でデータの詳細を確認しましょう。
dataset = load_breast_cancer()
# 特徴量 (説明変数)
X = pd.DataFrame(dataset.data,
columns=dataset.feature_names)
#ラベル(目的変数)
y = pd.Series(dataset.target, name='y')
# データ詳細確認
print('X shape: (%i,%i)' %X.shape)
print(y.value_counts())
display(X.join(y).head())X shape: (569,30)
1 357
0 212
Name: y, dtype: int64
mean radius mean texture mean perimeter mean area mean smoothness mean compactness mean concavity mean concave points mean symmetry mean fractal dimension radius error texture error perimeter error area error smoothness error compactness error concavity error concave points error symmetry error fractal dimension error worst radius worst texture worst perimeter worst area worst smoothness worst compactness worst concavity worst concave points worst symmetry worst fractal dimension y
0 17.99 10.38 122.80 1001.0 0.11840 0.27760 0.3001 0.14710 0.2419 0.07871 1.0950 0.9053 8.589 153.40 0.006399 0.04904 0.05373 0.01587 0.03003 0.006193 25.38 17.33 184.60 2019.0 0.1622 0.6656 0.7119 0.2654 0.4601 0.11890 0
1 20.57 17.77 132.90 1326.0 0.08474 0.07864 0.0869 0.07017 0.1812 0.05667 0.5435 0.7339 3.398 74.08 0.005225 0.01308 0.01860 0.01340 0.01389 0.003532 24.99 23.41 158.80 1956.0 0.1238 0.1866 0.2416 0.1860 0.2750 0.08902 0
2 19.69 21.25 130.00 1203.0 0.10960 0.15990 0.1974 0.12790 0.2069 0.05999 0.7456 0.7869 4.585 94.03 0.006150 0.04006 0.03832 0.02058 0.02250 0.004571 23.57 25.53 152.50 1709.0 0.1444 0.4245 0.4504 0.2430 0.3613 0.08758 0
3 11.42 20.38 77.58 386.1 0.14250 0.28390 0.2414 0.10520 0.2597 0.09744 0.4956 1.1560 3.445 27.23 0.009110 0.07458 0.05661 0.01867 0.05963 0.009208 14.91 26.50 98.87 567.7 0.2098 0.8663 0.6869 0.2575 0.6638 0.17300 0
4 20.29 14.34 135.10 1297.0 0.10030 0.13280 0.1980 0.10430 0.1809 0.05883 0.7572 0.7813 5.438 94.44 0.011490 0.02461 0.05688 0.01885 0.01756 0.005115 22.54 16.67 152.20 1575.0 0.1374 0.2050 0.4000 0.1625 0.2364 0.07678 0
上記からわかるようにScikit-Learn Cancer Datasetには説明変数(特徴量)が30、569のデータポイントがあります。
目的変数(ラベル)のうち"1"が良性の腫瘍、"0"が悪性の腫瘍を示します。
Cancer Datasetの前処理
Cancer Datasetの前処理として標準化を行います。
標準化とはデータの平均を0に、分散/標準偏差を1にする前処理であり、 各説明変数の目的変数選択への相関レベルを同一にします。
一つの説明変数の重要度に選択を引っ張られないようにすることと理解ください。
相関関係から良性、悪性の判断のために重要と思われる説明変数を絞り込む次元削減を前処理として行うことも多いですが、今回は説明変数の数が30しかないので次元削減は行いません。
from sklearn.preprocessing import StandardScaler
#StandardScalerにて標準化処理を行う
scaler = StandardScaler()
scaler.fit(X)
X_1 = pd.DataFrame(scaler.transform(X),columns=dataset.feature_names)
#標準化したX_1データを表示
display(X_1.join(y).head())mean radius mean texture mean perimeter mean area mean smoothness mean compactness mean concavity mean concave points mean symmetry mean fractal dimension radius error texture error perimeter error area error smoothness error compactness error concavity error concave points error symmetry error fractal dimension error worst radius worst texture worst perimeter worst area worst smoothness worst compactness worst concavity worst concave points worst symmetry worst fractal dimension y
0 1.097064 -2.073335 1.269934 0.984375 1.568466 3.283515 2.652874 2.532475 2.217515 2.255747 2.489734 -0.565265 2.833031 2.487578 -0.214002 1.316862 0.724026 0.660820 1.148757 0.907083 1.886690 -1.359293 2.303601 2.001237 1.307686 2.616665 2.109526 2.296076 2.750622 1.937015 0
1 1.829821 -0.353632 1.685955 1.908708 -0.826962 -0.487072 -0.023846 0.548144 0.001392 -0.868652 0.499255 -0.876244 0.263327 0.742402 -0.605351 -0.692926 -0.440780 0.260162 -0.805450 -0.099444 1.805927 -0.369203 1.535126 1.890489 -0.375612 -0.430444 -0.146749 1.087084 -0.243890 0.281190 0
2 1.579888 0.456187 1.566503 1.558884 0.942210 1.052926 1.363478 2.037231 0.939685 -0.398008 1.228676 -0.780083 0.850928 1.181336 -0.297005 0.814974 0.213076 1.424827 0.237036 0.293559 1.511870 -0.023974 1.347475 1.456285 0.527407 1.082932 0.854974 1.955000 1.152255 0.201391 0
3 -0.768909 0.253732 -0.592687 -0.764464 3.283553 3.402909 1.915897 1.451707 2.867383 4.910919 0.326373 -0.110409 0.286593 -0.288378 0.689702 2.744280 0.819518 1.115007 4.732680 2.047511 -0.281464 0.133984 -0.249939 -0.550021 3.394275 3.893397 1.989588 2.175786 6.046041 4.935010 0
4 1.750297 -1.151816 1.776573 1.826229 0.280372 0.539340 1.371011 1.428493 -0.009560 -0.562450 1.270543 -0.790244 1.273189 1.190357 1.483067 -0.048520 0.828471 1.144205 -0.361092 0.499328 1.298575 -1.466770 1.338539 1.220724 0.220556 -0.313395 0.613179 0.729259 -0.868353 -0.397100 0k-NNによる分類予測モデルの構築
k-NNを用いて標準化を行ったCancerDatasetの分類モデルを構築します。
Scikit-Learnにおけるtrain_test_splitを用いて訓練データとテストデータ用にX_1データを分割します。
今回は訓練データをX_1の80%(569x0.8=455)、テストデータをX_1の20%(569x0.2=114)とします。
またk-NNのハイパーパラメーターのうち、最も重要な判断のための最近傍点数を変数として訓練データの精度、テストデータの精度をリストに格納します。
from sklearn.neighbors import KNeighborsClassifier
#データセットをtest sampleを割合20%でホールドアウトする。
X_train, X_test, y_train, y_test = train_test_split(X_1,y, random_state=0, test_size=0.2)
#近傍オブジェクト数とその予測スコアを格納するリストを準備
List_n_neighbors = []
List_train_score = []
List_test_score = []
#近傍オブジェクト数を1-10で予測値を比較する。まずは訓練データに対してfitする。
for n_neighbors in range(1,11):
clf = KNeighborsClassifier(n_neighbors = n_neighbors).fit(X_train,y_train)
#訓練スコアと予測スコアを算出してリストに格納
List_n_neighbors.append(n_neighbors)
List_train_score.append(clf.score(X_train,y_train))
List_test_score.append(clf.score(X_test,y_test))訓練データ、テストデータの予測精度の可視化
パラメータとしたk-NNの近傍点数kをx軸、訓練データの精度/テストデータの精度をy軸にしてmatplotで可視化します。
#近傍オブジェクト数に対して訓練、テストスコアをプロットする
fig = plt.figure(figsize = (10,6))
plt.plot(List_n_neighbors, List_train_score, label = "training accuracy")
plt.plot(List_n_neighbors, List_test_score, label = "test accuracy")
plt.ylabel("Accuracy")
plt.xlabel("n_neighbors")
plt.xticks(np.linspace(1,11,11))
plt.legend()<matplotlib.legend.Legend at 0x7f6d8354a5c0>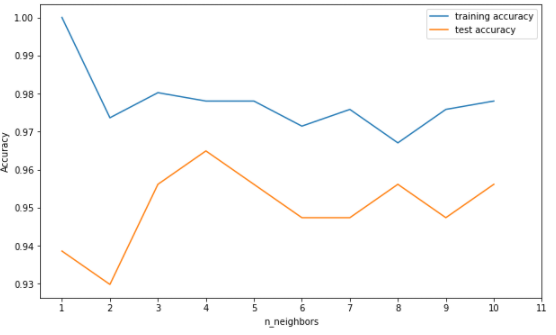
Cancer Datasetを用いた予測においては近傍オブジェクト数(k)がk=4あたりが最良の性能であることがうかがえます。
ただしK=2の場合でも93%程度の精度が確保されており、特徴量30程度のCancer Datasetに関してはNearest Neighbor Classificationによる分類は十分に機能しているように見えます。
分類モデルの評価指標での確認
以下classification_reportによる結果を確認しても再現率(recall)、適合率(precision)ともに大きな偏りなく精度を保っていることが確認できます。
ただし実際にガンの診断に使えるかというと以下classification_reportによる結果を確認すると悪性腫瘍の再現率(recall)の精度から悪性47件のうち3件程度は悪性腫瘍を良性と判断してしまう点から残念ながら難しいと思われます。
clf = KNeighborsClassifier(n_neighbors = 4).fit(X_train,y_train)
predict_result = clf.predict(X_test)
print(classification_report(y_test,predict_result, target_names=["悪性","良性" ])) precision recall f1-score support
悪性 0.98 0.94 0.96 47
良性 0.96 0.99 0.97 67
accuracy 0.96 114
macro avg 0.97 0.96 0.96 114
weighted avg 0.97 0.96 0.96 114
実際に活用できるレベルにするにはかなりの精度が必要なんだね、、
まとめ
本日はk-NN法の分類基礎について解説しました。
実務上で活躍することはないようですが、機械学習の分類手法としてはどの書籍にもある重要なものです。
今回は分類を扱いましたが同様にk-NN Regressionという回帰を扱うモデルもあります。
興味のある方はScikit-Learnのサイトで確認してみましょう!
本日は以上です。
今日があなたのスタートの日。明るい未来に向けて一緒に頑張りましょう!