Python データサイエンス 統計

【Python/Scipy】正規分布かどうかを定量的に確認する方法

脳みそ男

手元のデータが正規分布かどうかを定量的に確認するにはどうしたらいい？

正規分布であることを確認することでどんなメリットがあるの？

脳筋太郎
'

本記事ではそんな疑問に対してサンプルコードを添えてお答えします。

回帰予測を行う際に目的変数が正規分布にしたがっているのかどうか確認することは精度向上のために非常に重要です。
本記事ではデータをヒストグラム等で可視化した際に実際にどの程度正規分布に一致するのかそれとも逸脱しているのかを定量的に確認する方法を説明します。

最後まで読めば手元のデータが簡単に正規分布かどうかを確認することができますので是非参考にしてください。

それでは始めましょう！

こんな方におすすめの記事

  • データを正規分布に変換することによるメリットを知りたい方
  • 正規分布かどうかを確認する検定手法を知りたい方


数値データを正規分布にすることによるメリット


正規分布かどうかの検定について説明する前にまずはデータが正規分布であることがなぜ嬉しいのか説明します。

まず、回帰予測時に目的変数が正規分布であることで予測残渣の正規分布性を期待するモデル適用時の精度向上が見込めます。

予測残渣の正規分布性を期待するモデルとは線形回帰などのことです。線形回帰は正規分布のデータを仮定した予測モデルになるため、目的変数を正規分布に近づけることで精度が上がります。

その他にも数値データの説明変数を適切に加工することで有用な説明変数を作成することができます。


一方で決定木などのモデルでは大小関係のみが学習に影響するので、データを正規分布に変換したとしても学習にはほとんど影響はないのでその点は理解しておきましょう。

正規分布であることのメリット

  • 目的変数が正規分布であることで予測残渣の正規分布性を期待するモデル適用時（線形回帰 等)の精度向上が見込める
  • 説明変数の数値データを正規分布に近づけることで有用な特徴量となる場合がある


今回の本題ではないので細かい説明は省きますが、数値データを正規分布に変換するための手法として以下があります。

  • 対数変換 (←まずトライすべき方法)
  • Box-Cox変換
  • Yeo-Johnson変換 (←負の値をもつデータにも適用可能)



正規分布かどうかを定量的に確認する方法


では本題として正規分布かどうかを定量的に確認する方法に関して説明します。
正規分布かどうかを確認する方法として以下が挙げられます。

  • QQプロットによる可視化
  • シャピロウィルク検定


それぞれ順番に説明します。

QQプロットによる可視化


QQプロットとは観測値が正規分布に従う場合の期待値をY軸、観測データをX軸にとった確率プロットのことです。
簡単に言えば「観測データと正規分布の類似度を可視化した図」であり、プロットが一直線上に並べば、観測値は正規分布に従っていると考えられます。

以下のサイトのアニメーションが非常にわかりやすいです↓

Qiita -> https://qiita.com/kenmatsu4/items/59605dc745707e8701e0


シャピロウィルク検定


シャピロウィルク検定とはランダムに取得された\(x_{1}, x_{2}, \ldots, x_{n}\)に対して以下の数式から統計量\(W\)を計算し、正規分布に従うか仮説検定を行う手法になります。

算出された統計量\(W\)(statistic)が小さい場合は正規分布から逸脱しており、大きい場合は正規分布に類似していることを示します。

$$
W=\frac{\left(\sum_{i=1}^{n} a_{i} x_{(i)}\right)^{2}}{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}}
$$



詳細は省きますがここにおける\(a\)はデータの平均や分散から算出される定数です。

scipy.stats.shapiro -> https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.shapiro.html

nderson-Darling and Shapiro-Wilk tests -> https://www.itl.nist.gov/div898/handbook/prc/section2/prc213.htm



PythonによるQQプロット/シャピロウィルク検定


それでは実際にQQプロット/シャピロウィルク検定を実装してみましょう！
以下に検定用のサンプルコードを記載します。

入力

def get_check_norm(x:pd.Series):
    """show norm feature with Sapiro-Wilk test

    Args:
        x (pd.Series): Pandas Series
    Returns:
        p : scipy.stats.shapiro
    """
    plt.hist(x, bins=100)#ヒストグラム表示
    plt.pause(.01)
    stats.probplot(x, dist="norm", plot=plt)#QQプロット表示
    plt.pause(.01)
    p=stats.shapiro(x)#シャピロウィルク検定
    print(p)

    return p

今回はscikit-leranのcalifornia_housingのデータセットを利用します。
以下のコードからデータセットを読み込みましょう。


入力

#Calfornia hosing dataの読み込み
# サンプルデータの取得
data = sklearn.datasets.fetch_california_housing()
df_1=pd.DataFrame(data.data, columns=data.feature_names)
df_1["Price"]=data.target



本データセットの人口(Population)を対象にまずはデータ変換なしにQQプロット/シャピロウィルク検定を実行してみましょう。
上記の関数を利用して以下で実行します。


入力

#検定の実行
shapiro=get_check_norm(df_1.Population)

出力

ShapiroResult(statistic=0.7133157253265381, pvalue=0.0)


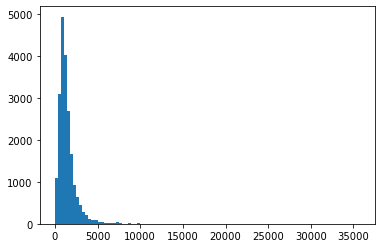
上図がデータの分布、下図がQQプロットになります。
データの分布を見ると右に裾が長い形状になっているため、正規分布とはかけ離れています。実際にQQプロットを見ても特に少ない人口帯、多い人口帯で正規分布から逸脱しているのが見て取れます。
実際にscipy.shapiroにて算出された統計量\(W\)は0.71となっています。
scipy.shapiroではN>5000以上のデータではp値が正しく算出されないと記載あるため、今回p値を利用しての検定に対する深堀りは避けます。

ではデータを正規分布に近づけた上でもう一度QQプロット/シャピロウィルク検定を実行してみましょう。
今回は簡単のために人口(Population)を対数変換して正規分布に近づけてみたいと思います。
以下が実行結果です。

入力

#対数変換
log_population=np.log(df_1.Population)

#検定の実行
shapiro=get_check_norm(log_population)

出力

ShapiroResult(statistic=0.9389429092407227, pvalue=0.0)


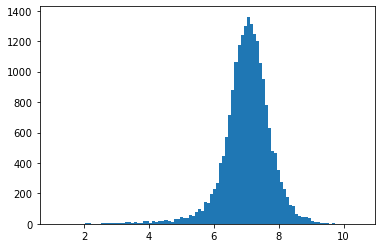
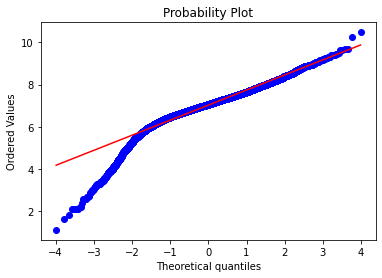
QQプロットを見ると少ない人口帯を除いては正規分布に近づいていることがわかります。
実際に算出された統計量\(W\)も0.94と先程よりも大きい値となっています。

まとめ


今回はデータが正規分布に近いかどうかをscipyを利用して定量的に確認する方法に関してまとめました。

データが正規分布に近いことで何かと便利なことが多いので、ぜひ本記事での検証方法を利用してみてください。


もっと詳しくPythonの使い方を勉強したいと思ったそこのアナタ！pythonを用いたコーディング学習にはData Campがおススメです！

詳細に関してはこちらで紹介しています。↓

こちらもぜひ参考にしてください。


それでは本日は以上でした！

-Python, データサイエンス, 統計