統計検定２級に最短で合格する方法【チートシート有り】

統計検定はデータサイエンティストとしての登竜門として、オススメの資格です！

昨今の機械学習モデル構築においては特に統計の知識がなくともモデリングできてしまいますが、やはり原理原則を理解することでその扱い方法に差がでてきます。

大量のデータを扱う機会が多くなってきた現代だからこそ求められる統計の知識！まずは統計検定２級を取得してデータサイエンティストとしての１歩を踏み出しましょう！

それでは始めましょう！

統計検定２級に最短で合格するための勉強ステップ

最短で統計検定2級に合格するためには以下の勉強ステップを参考にしてください。

最短で合格を目指すならいきなり分厚い解説本を気合い入れて読み始めるのはおすすめしません。

まずは手を動かしてわからない部分を解説本で知識を補完していくのが、効率的です。

統計検定２級を受験するに際しては以下の参考書がおすすめです！

統計検定受験のポイント【チートシート】

私自身が統計検定２級を受験した際にチートシートとしてポイントをまとめたものを共有します。

高頻度で出題されるポイントに絞ったので受験の際の参考にしていただければ幸いです。

本チートシート作成に関しては大いに以下のBellCurve様のサイトを参考にしています。

主な統計用語と定義

ローレンツ曲線

確率度数分布における指標別の累積相対度数をそれぞれプロットしたグラフをローレンツ曲線と呼ぶ。

完全平等線とローレンツ曲線の範囲の面積をジニ係数と呼び、不平等差を定量化する指標として用いられる。

分散・標準偏差

各データの値と平均値の差の2上をすべて足した値の平均値を分散と呼び、以下で示す。データのばらつき度合いを示す指標のこと。

\begin{aligned} V=\frac{1}{n} \sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}\end{aligned}

分散の平方根を取った値を標準偏差と呼ぶ。

\begin{aligned} \sigma=\sqrt{\frac{1}{n} \sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}}\end{aligned}

変動係数

平均が大きく異なるデータ同士の標準偏差の比較を行う際に取る指標。

変動係数 = 標準偏差 ÷平均値

\begin{aligned}CV=\frac{\sigma}{\bar{x}}\end{aligned}

歪度・尖度

歪度(わいど）　：対象の分布が正規分布から左右にどれだけ歪んでいるかを示す指標。

「右裾が長い」もしくは「右に歪んだ」もしくは「左に偏った」分布のときには正の値を、「左裾が長い」もしくは「左に歪んだ」もしくは「右に偏った」分布のときには負の値をとる。

\begin{aligned}\frac{n}{(n-1)(n-2)} \sum_{i=1}^{n}\left(\frac{x_{i}-\bar{x}}{s}\right)^{3}\end{aligned}

尖度（せんど）　：分布が正規分布からどれだけ尖っているかを表す指標。

正規分布より尖った分布（データが平均付近に集中し、分布の裾が重い）のときには正の値を、正規分布より扁平な分布（データが平均付近から散らばり、分布の裾が軽い）のときには負の値をとる。

\begin{aligned}\frac{n(n+1)}{(n-1)(n-2)(n-3)} \sum_{i=1}^{n} \frac{\left(x_{i}-\bar{x}\right)^{4}}{s^{4}}-\frac{3(n-1)^{2}}{(n-2)(n-3)}\end{aligned}

箱ひげ図

四分位数を可視化したグラフのこと。

四分位数はデータを小さい順に並べて、小さいものから順位を付けた時に、

• 25％（全体の1/4の部分）＝25パーセンタイル
• 50％（全体の2/4＝1/2の部分）＝50パーセンタイル
• 75％（全体の3/4の部分）＝75パーセンタイル

に該当する値のこと。

ベン図

集合を視覚的に表す場合に用いる図示方法。

条件付き確率

事象Bが起こるという条件のもとで事象Aが起こる場合、この条件付き確率\(P(A \mid B)\)を以下で示す。

\begin{aligned}P(A \mid B)=\frac{P(A \cap B)}{P(B)}\end{aligned}

推定量の一致性と不偏性

一致性

推定量を元に母平均や母分散のような分布のパラメータ（母数）を推測するとき、その推測が正確である必要がある。大数の法則は、サンプルサイズnが大きくなると、標本平均が母平均に近づくという原則である。このように、nが大きくなれば、推定量がだんだんと真のパラメータに近づく性質を「一致性」とよぶ。

不偏性

推定量を元に母平均や母分散のような分布のパラメータ（母数）を推測するとき、その推測が真のパラメータから大きく外れてしまっては意味がない。言い換えると、推定量の期待値がパラメータに一致する必要がある。この性質を「不偏性」と呼ぶ。

標本分散と不偏分散

標本分散

標本分散は一致推定量ではあるものの不偏推定量ではない。つまり、nが十分に大きくない場合には標本分散の期待値は母分散に一致せず、母分散より小さくなる。

$$\widehat{\sigma}^{2}=\frac{1}{n} \sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}$$

不偏分散

標本分散の期待値が母分散に一致するように標本分散の算出式にn/(n-1)をかけたものが不偏分散の算出式となる。したがって、不偏分散は一致性と不偏性をもつ推定量となる。

$$s^{2}=\frac{n}{n-1} \times \frac{1}{n} \sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}=\frac{1}{n-1} \sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}$$

標準偏差と標準誤差

標準偏差

$$\begin{aligned}s=\sqrt{\frac{1}{n-1} \sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}}\end{aligned}$$

標準誤差（SE)

定量の標準偏差であり、標本から得られる推定量そのもののバラつき（＝精度）を表す。標準誤差は、一般的に「標本平均の標準偏差」を意味する。

$$\begin{aligned}S E=\frac{s}{\sqrt{n}}=\frac{\sqrt{\frac{1}{n-1} \sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}}}{\sqrt{n}}\end{aligned}$$

決定係数

決定係数は、説明変数が目的変数をどれくらい説明しているか、つまり「回帰変動が全変動に対してどれだけ多いか＝残差変動が全変動に対してどれだけ少ないか」を表すもの。

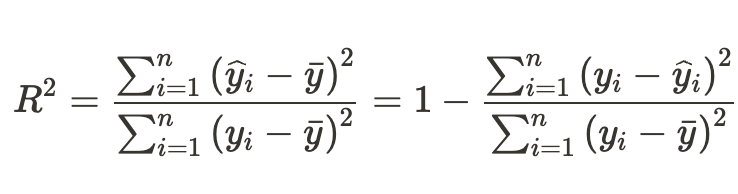
フィッシャーの３原則

• 繰り返し (反復 repetition)1回だけの実験ではどの程度の誤差がある処理なのか分からないので、何回も実験をすること。偶然誤差の大きさを評価することができる。
• 無作為化 (ランダム化 randomization)実験結果に影響を与えかねない要因（時刻、気温、日照etc）が、なるべくバラバラになるよう割り当てること。系統誤差を偶然誤差に転化することができる。
• 局所管理 (local control)実験結果に影響を与えかねない要因（実験場所、時間帯、担当者etc）を、実験のブロック内ではできるだけ均一になるように実験ブロックを小分けにすること。系統誤差も分散分析の要因に取り込むことができる。
  
  
  

標本の抽出方法

層化抽出法

母集団をあらかじめいくつかの層（グループ）に分けておき、各層の中から必要な数の調査対象を無作為に抽出する方法

クラスター抽出法

次の1～3によって調査対象を抽出する方法

1. 母集団を、小集団である「クラスター（集落）」に分ける
2. 分けられたクラスターの中から、いくつかのクラスターを無作為抽出する
3. それぞれのクラスターにおいて全数調査を行う

多段抽出法

母集団をいくつかのグループに分け、そこから無作為抽出でいくつかグループを選ぶ事を繰り返し、最終的に選ばれたグループの中から調査対象を無作為抽出する方法。

二層抽出法

層化抽出を行いたいが母集団の情報がない場合、まず母集団から標本を抽出して母集団の情報を取得し、その情報をもとに層化抽出を行う方法。

系統抽出法

母集団に通し番号を付け、等間隔で標本を抽出する方法。

各種公式および定理

条件付き確率 乗法定理

$$P(A \cap B)=P(B) \times P(A \mid B)$$

$$P(A \cap B)=P(A) \times P(B \mid A)$$

ベイズの定理

\(P(B_{i})\)を事前確率、\(P(B_{i} \mid A)\)を事後確率と呼ぶ。

\begin{aligned}P\left(B_{i} \mid A\right)=\frac{P\left(A \cap B_{i}\right)}{P(A)}=\frac{P\left(B_{i}\right) P\left(A \mid B_{i}\right)}{\sum P\left(B_{j}\right) P\left(A \mid B_{j}\right)}\end{aligned}

離散型確率変数・連続型確率変数の期待値

離散型確率の期待値

$$\begin{aligned}E(X)=\sum_{i=1}^{n} x_{i} \times p_{i}\end{aligned}$$

連続型確率変数の期待値

$$\begin{aligned}E(X)=\int_{-\infty}^{\infty} x f(x) d x\end{aligned}$$

期待値の性質

$$E[X+k] =E[X]+k$$

$$E[k X] =k E[X] $$

$$E[X+Y] =E[X]+E[Y] $$

$$E[X-Y] =E[X]-E[Y] $$

$$E[X Y] =E[X] E[Y]+\operatorname{Cov}[X, Y] $$

$$E\left[X^{2}\right] =E[X]^{2}+V[X] =\int_{-\infty}^{\infty} x^{2} f(x) d x$$

離散型確率変数・連続型確率変数の分散

離散型確率変数の分散

$$\begin{aligned}V(X)=\sum_{i=1}^{n}\left(x_{i}-\mu\right)^{2} p_{i}\end{aligned}$$

連続型確率変数の分散

$$\begin{aligned}V(X)=\int_{-\infty}^{\infty}(x-\mu)^{2} f(x) d x\end{aligned}$$

分散の性質

$$V[X] =\frac{1}{n} \sum\left(x_{i}-E[X]\right)^{2} =E\left[X^{2}\right]-E[X]^{2} $$

$$V[X+k] =V[X] $$

$$V[k X] =k^{2} V[X] $$

$$V[X+Y] =V[X]+V[Y]+2 \operatorname{Cov}[X, Y] $$

$$V[X-Y] =V[X]+V[Y]-2 \operatorname{Cov}[X, Y]$$

2変数の期待値と分散

確率変数X,Yにおける変数間の関係の強さを表す共分散は以下で定義される。

$$\operatorname{Cov}(X, Y)=E\left[\left(X-\mu_{x}\right)\left(Y-\mu_{y}\right)\right]$$

$${Cov}[X, Y] =E[XY] -E[X]E[Y]$$

$$2 \operatorname{Cov}[X, Y] =V[X+Y]-V[X]-V[Y] $$

$$-2 \operatorname{Cov}[X, Y] =V[X-Y]-V[X]-V[Y] $$

$$\operatorname{Cov}[X, X] =V[X]$$

この共分散から相関係数は以下で定義される。

$$\rho=\frac{\operatorname{Cov}(X, Y)}{\sqrt{V(X) V(Y)}}$$

大数の法則

多数回の試行の結果として得られたデータの平均（標本平均）や相対度数が試行回数ｎを大きくするとき確率分布の平均（母平均）や生起確率に近づくことを保証する理論的根拠となる法則。

中心極限定理

標本を抽出する母集団が平均\(\mu\)、分散\(\sigma^2\)の正規分布に従う場合においても、従わない場合においても、抽出するサンプルサイズnが大きくなるにつれて標本平均の分布は「平均\(\mu\)、分散\(\sigma^2/n\)」の正規分布に近づくという定理。

標本を抽出する母集団が平均\(\mu\)、分散\(\sigma^2\)の正規分布を標準化した

$$\begin{aligned}z=\frac{\bar{x}-\mu}{\sqrt{\frac{\sigma^{2}}{n}}}=\frac{\bar{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\end{aligned}$$

の分布はサンプルサイズが大きくなるにつれて標準正規分布\(N(0,1)\)に近づく。

ベイズの定理

\(P(B_{i})\)を事前確率、\(P(B_{i} \mid A)\)を事後確率と呼ぶ。

\begin{aligned}P\left(B_{i} \mid A\right)=\frac{P\left(A \cap B_{i}\right)}{P(A)}=\frac{P\left(B_{i}\right) P\left(A \mid B_{i}\right)}{\sum P\left(B_{j}\right) P\left(A \mid B_{j}\right)}\end{aligned}

代表的な確率分布

二項分布

ベルヌーイ試行

「コインを投げたときに表が出るか裏が出るか」のように、何かを行ったときに起こる結果が2つしかない試行のこと。

$$P(X=1)=p$$

$$ P(X=0)=1-p$$

ベルヌーイ試行をｎ回行って、成功する回数が従う確率分布を二項分布と呼ぶ。

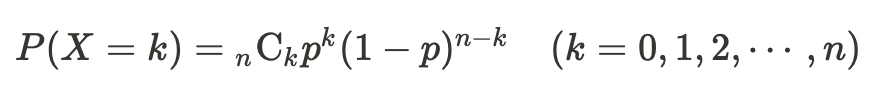
二項分布の期待値と分散

$$E(X)=n p $$

$$V(X)=n p(1-p)$$

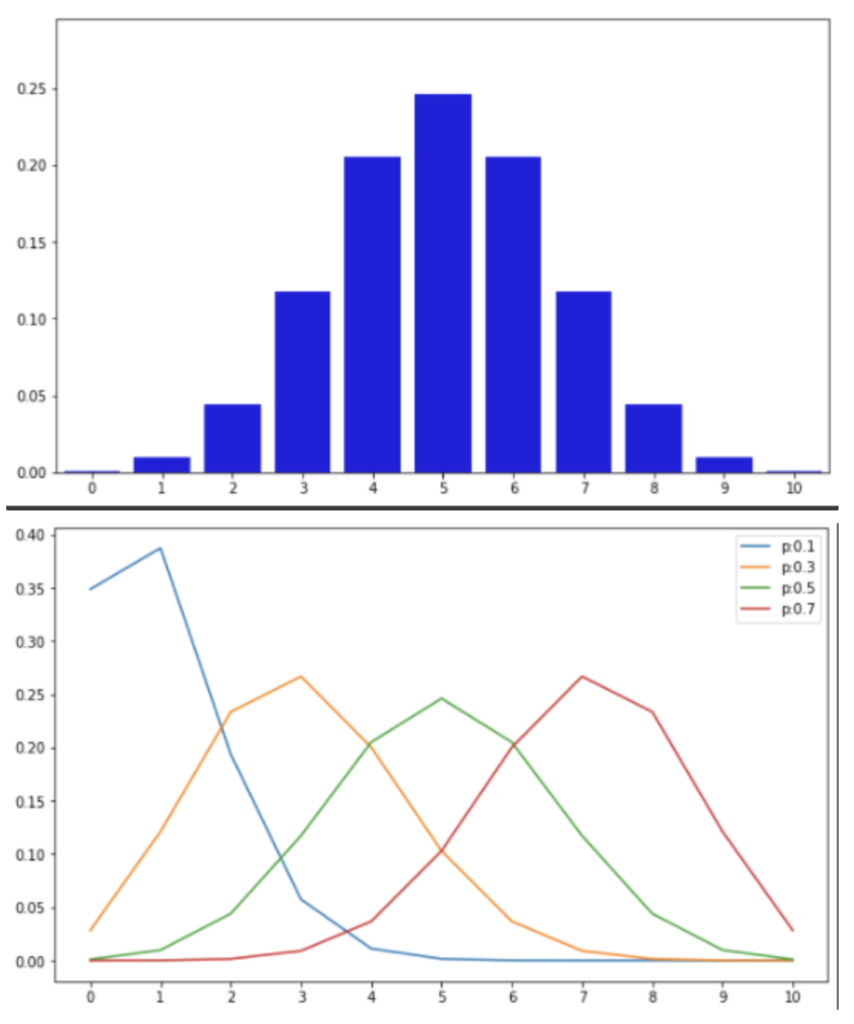
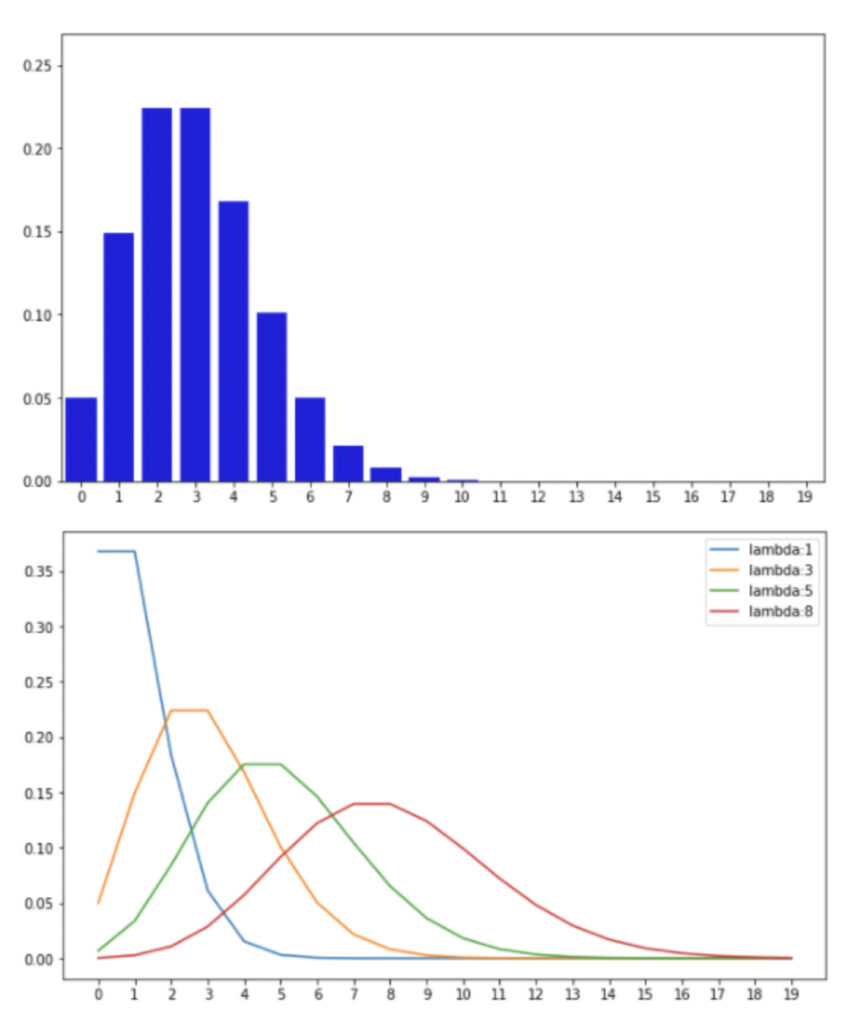
ポアソン分布

交通事故や故障品の発生率などnが十分大きく確率pが非常に小さい場合、「np=一定」と考えることができる。そこで\(np=\lambda\)とおくと、事故が起こる回数は「ポアソン分布」に従う。

$$\begin{aligned}P(X=k)=\frac{e^{-\lambda} \lambda^{k}}{k !} \quad(k=0,1,2, \cdots)\end{aligned}$$

ポアソン分布の期待値と分散

$$E(X)=\lambda $$

$$V(X)=\lambda$$

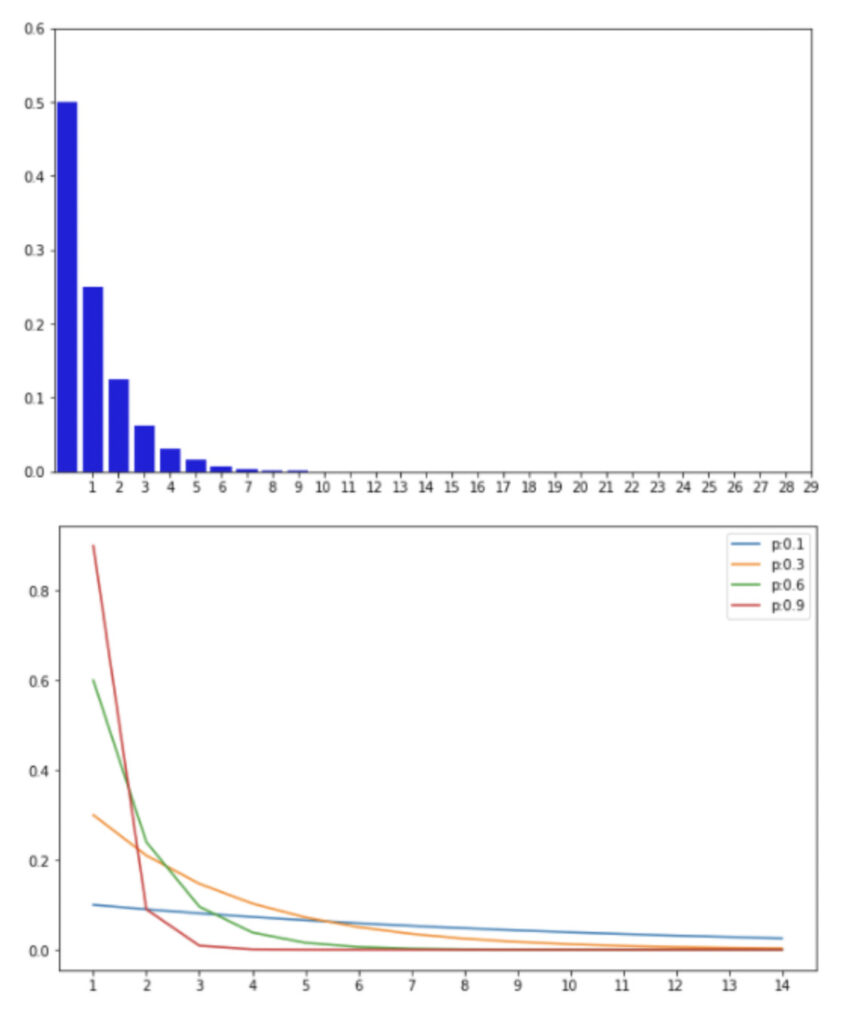
幾何分布

成功確率がである独立なベルヌーイ試行を繰り返す時、初めて成功するまでの試行回数が従う確率分布のこと。

$$P(X=k)=(1-p)^{k-1} p \quad(k=1,2,3, \cdots)$$

幾何分布の期待値と分散

$$E(X)=\frac{1}{p} $$

$$V(X)=\frac{1-p}{p^{2}}$$

正規分布

正規分布は統計学における検定や推定、モデルの作成など様々な場面で活用される連続型確率分布である。

正規分布の確率密度関数は以下で示される。

$$\begin{aligned}f(x)=\frac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{(x-\mu)^{2}}{2 \sigma^{2}}} \quad(-\infty<x<\infty)\end{aligned}$$

正規分布の期待値と分散

$$E(X)=\mu$$

$$V(X)=\sigma^{2}$$

正規分布の再生性

正規分布\(N\left(\mu_{1}, \sigma_{1}^{2}\right)\)に従うあるデータと、そのデータとは独立な正規分布\(N\left(\mu_{2}, \sigma_{2}^{2}\right)\)に従うデータを足したデータは、正規分布\(N\left(\mu_{1}+\mu_{2}, \sigma_{1}^{2}+\sigma_{2}^{2}\right)\)に従う。

正規分布の標準化

ある確率変数が平均\(\mu$、分散$\sigma^2\)の正規分布に従う時以下で標準化することで「平均が0、分散が1の標準正規分布」に従う。

$$\begin{aligned}z=\frac{X-\mu}{\sigma}\end{aligned}$$

指数分布

指数分布は連続型確率分布の一つで、機械が故障してから次に故障するまでの期間や、災害が起こってから次に起こるまでの期間のように、次に何かが起こるまでの期間が従う分布のこと。

$$f(x)= \begin{cases}\lambda e^{-\lambda x} & x \geq 0 \ 0 & x<0\end{cases}$$

指数分布の期待値と分散

$$E(X)=\frac{1}{\lambda}$$

$$V(X)=\frac{1}{\lambda^{2}}$$

指数分布の累積確率分布関数

$$F(x)=P(X \leq x)=\int_{-\infty}^{x} f(t) d t=\int_{0}^{x} \lambda e^{-\lambda t} d t=1-e^{-\lambda x}$$

離散一様分布

離散一様分布は、確率変数が離散型である場合に、すべての事象の起こる確率が等しい分布のこと。

$$\begin{aligned}P(X=k)=\frac{1}{N} \quad(k=1,2, \cdots, N)\end{aligned}$$

離散一様分布の期待値と分散

$$E(X) =\frac{N+1}{2} $$

$$V(X) =\frac{N^{2}-1}{12}$$

連続一様分布

確率変数がどのような値でも、その時の確率密度関数が一定の値をとる分布のことを連続一様分布と呼ぶ。

$$f(x)=\frac{1}{b-a} \quad(a \leq X \leq b) $$

$$f(x)=0 \quad(Xb)$$

連続一様分布の期待値と分散

$$E(X)=\frac{a+b}{2} $$

$$V(X)=\frac{(b-a)^{2}}{12}$$

区間推定

標本平均における区間推定（母分散/母平均既知）

区間推定手順

1. 標本平均\(\bar x\)を求める。
2. 標本平均の標準化を行う。

$$\begin{gathered}\frac{\bar{x}-\mu}{\sqrt{\frac{\sigma^{2}}{n}}}\end{gathered}$$

1. 2. で標準化した値が標準正規分布の95%面積の範囲にあることを確認する。
   
   

$$\begin{gathered}-1.96 \leq \frac{\bar{x}-\mu}{\sqrt{\frac{\sigma^{2}}{n}}} \leq 1.96\end{gathered}$$

$$\begin{gathered}\bar{x}-1.96 \times \sqrt{\frac{\sigma^{2}}{n}} \leq \mu \leq \bar{x}+1.96 \times \sqrt{\frac{\sigma^{2}}{n}}\end{gathered}$$

標本平均における区間推定 t分布（母平均のみ既知）

未知である母分散\(\sigma^2\)の代わりに普遍分散\(s^2\)を用いる。

この条件のもと次に示される統計量tの値は自由度n-1のt分布に従う。

$$\begin{gathered}t=\frac{\bar{x}-\mu}{\sqrt{\frac{s^{2}}{n}}}\end{gathered}$$

標準正規分布N(0, 1)に従うZと自由度nのカイ二乗分布Wがあり、これらが互いに独立であるとき、次の式から算出されるtは自由度nのt分布に従う。

$$\begin{gathered}t=\frac{Z}{\sqrt{\frac{W}{n}}}\end{gathered}$$

確率変数\(X\)が自由度mのt分布に従っているとき\(X\)の期待値、分散は次で示される。

$$E(X)=0 \quad(m>1) $$

$$V(X)=\frac{m}{m-2} \quad(m>2)$$

母平均の信頼区間

$$\begin{gathered}\bar{x}-t_{\alpha / 2}(n-1) \times \sqrt{\frac{s^{2}}{n}} \leq \mu \leq \bar{x}+t_{\alpha / 2}(n-1) \times \sqrt{\frac{s^{2}}{n}}\end{gathered}$$

母比率の信頼区間

母平均の推定と同じように、母比率についても区間推定を行うことができる。成功確率がpである試行をn回行うときに成功する回数をXとすると、Xは二項分布\(B(n,p)\)に従う。このpが母比率に対応する。

二項分布に従う確率変数\(X\)の期待値と分散は次で示される。

$$E(X)=n p$$

$$V(X)=n p(1-p)$$

nがある程度大きいときは\(B(n,p)\)は正規分布\(N(np,np(1-p))\)に従うと近似できる。

$$\begin{gathered}Z=\frac{X-n p}{\sqrt{n p(1-p)}}\end{gathered}$$

標本比率\(\hat p\)は\(X/n\)から求められる。したがって

$$\begin{gathered}Z=\frac{\widehat{p}-p}{\sqrt{\frac{p(1-p)}{n}}}\end{gathered}$$

95%信頼区間は以下で示すことができる。

$$\begin{gathered}\widehat{p}-1.96 \times \sqrt{\frac{\widehat{p}(1-\widehat{p})}{n}} \leq p \leq \widehat{p}+1.96 \times \sqrt{\frac{\widehat{p}(1-\widehat{p})}{n}}\end{gathered}$$

母比率の差の信頼区間

母比率の信頼区間は以下で求めることができる。

$$\widehat{p_{1}}-\widehat{p_{2}} \sim N\left(p_{1}-p_{2}, \frac{p_{1}\left(1-p_{1}\right)}{n_{1}}+\frac{p_{2}\left(1-p_{2}\right)}{n_{2}}\right)$$

$$\begin{aligned}&\left(\widehat{p_{1}}-\widehat{p_{2}}\right)-z_{\frac{\alpha}{2}} \times \sqrt{\frac{\widehat{p_{1}}\left(1-\widehat{p_{1}}\right)}{n_{1}}+\frac{\widehat{p_{2}}\left(1-\widehat{p_{2}}\right)}{n_{2}}} \leq p_{1}-p_{2} \leq\left(\widehat{p_{1}}-\widehat{p_{2}}\right)+z_{\frac{\alpha}{2}}\end{aligned} $$

$$\begin{aligned}\times \sqrt{\frac{\widehat{p_{1}}\left(1-\widehat{p_{1}}\right)}{n_{1}}+\frac{\widehat{p_{2}}\left(1-\widehat{p_{2}}\right)}{n_{2}}}\end{aligned}$$

必要なサンプルサイズ

事前確率pが与えられているとき信頼区間5%以下にするために必要なサンプルサイズnを以下で求める事ができる。

$$\begin{gathered}2 \times 1.96 \times \sqrt{\frac{p(1-p)}{n}} \leq 0.05\end{gathered}$$

カイ二乗分布

カイ二乗分布は自由度kの\(\chi^2\)が従う確率分布として以下で示すことができる。

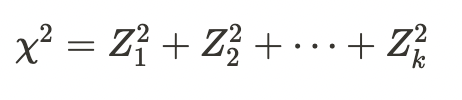
期待値、分散は以下で示すことができる。

$$E(X)=k $$

$$V(X)=2 k$$

母分散の信頼区間

母分散の区間推定では正規分布やt分布ではなく、カイ二乗分布を用いる。

母集団が母分散の正規分布に従う時、抽出された標本のサンプルサイズをn、不偏分散を$s^2$として自由度n-1のカイ二乗分布に従うことを用いて母分散の信頼区間を計算する。

$$\begin{aligned}\chi^{2}=\frac{(n-1) s^{2}}{\sigma^{2}}\end{aligned}$$

カイ二乗分布における上側2.5%、下側2.5%は以下で確認することができる。

$$\begin{aligned}2.70 \leq \frac{(n-1) s^{2}}{\sigma^{2}} \leq 19.02\end{aligned}$$

仮説検定

関連語彙

帰無仮説

検定の最初に立てる仮説のこと、この仮説を元に検定を行い結論を導く。\(H_0\)と書かれる。

対立仮説

帰無仮説に対する仮説のこと、本来証明したい仮説。\(H_1\)と書かれる。

検定統計量

帰無仮説が正しいと仮定したときに、観測した事象よりも稀なことが起こる確率を計算するための値。

p値

帰無仮説が正しいとした仮定とき、観測した事象よりも極端なことが起こる確率。「観測した事象よりも極端な事象が起こる確率」であることから、これは累積確率となる。

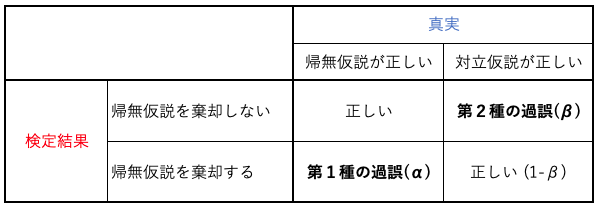
有意水準

有意水準は、検定において帰無仮説を設定したときにその帰無仮説を棄却する基準となる確率のこと。（アルファ）で表され、5%（0.05）や1%（0.01）といった値がよく使われる。

検出力

有意水準と対するものとして、「検出力」がある。検出力は\(1-\beta\)で表されるもので、「帰無仮説が正しくないときに、正しくを棄却する確率」のことを示す。

２標本t検定

2つの独立した母集団があり、それぞれの母集団から抽出した標本の平均に差があるかどうかを検定することを「2標本t検定」という。

1群目の標本平均を\(\bar x_1\)、母平均\(\mu_1\)を、サンプルサイズを\(n_1\)、2群目の標本平均を\(\bar x_2\)、母平均を\(\mu_2\)、サンプルサイズを\(n_2\)としたときに、次の式から算出される統計量tを使う。検定で用いるのは自由度\((n_1+n_2-1)\)のt分布である。

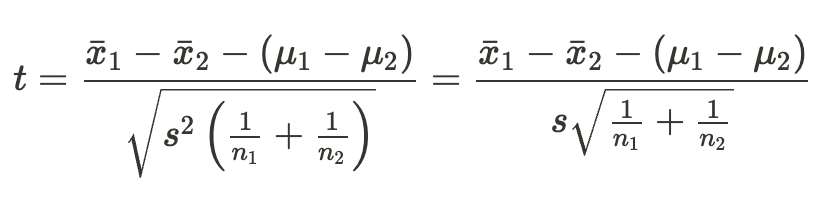
上記計算においてはプールした分散を用いる。

$$\begin{aligned}s^{2}=\frac{\left(n_{1}-1\right) \times s_{1}^{2}+\left(n_{2}-1\right) \times s_{2}^{2}}{n_{1}+n_{2}-2}\end{aligned}$$

ポアソン分布を用いた検定

次の統計量が標準正規分布に従うとして検定を行う。

$$\begin{aligned}z=\frac{\frac{X}{n}-\lambda}{\sqrt{\frac{\lambda}{n}}}\end{aligned}$$

まとめ

今回は統計検定２級合格の方法および頻出項目に関するチートシートをまとめました。

少しでも参考にしていただければ幸いです。

pythonなどを活用した解析手法が発達したため、統計を深く理解していなくともそれっぽい結果を出すことはとても簡単になりました。

しかしやはり本質を理解しているのといないのとでは説明に圧倒的な差が出ます。

血の通ったデータサイエンティストを目指すためにも統計の勉強をおすすめします！

統計も理解した上でもっと詳しくPythonの使い方を勉強したいと思ったそこのアナタ！pythonを用いたコーディング学習にはData Campがおススメです！

詳細に関してはこちらで紹介しています。↓

こちらもぜひ参考にしてください。

【無料体験あり】最速でデータサイエンティスト基礎を学ぶ方法【DataCamp】

脳みそ男 プログラミングの勉強を始めたいけど何から始めればよいのか分からない！ どうせ必要ならプログラミングと英語の勉強 ...

それでは本日は以上でした！