こんにちは、TaKiです!
本日は決定木(Decision Tree )モデルを用いた機械学習手法について紹介します。

機械学習を導入したいけど、予測精度がでる理由が説明できないと使えないなぁ、、
なるべくデータの前処理の手間を減らして予測モデルを構築したい!

本記事ではそんな疑問にお答えします。
決定木モデルを用いた機械学習では最低限のデータ前処理で比較的高い精度を出すことができます!
また予測値における説明変数の重要度を簡単に定量化、可視化することができる点において実務活用にも最適です!
本日はそんな決定木モデルの原理、メリット/デメリット、実際の予測モデルのコーディングを紹介していきます、ぜひ最後まで学んでいってください!
こんな方におすすめの記事
- 予測結果を説明できる機械学習モデルを構築したい
- 決定木モデル分析の基礎をコーディングで学びたい
- とりあえずのデータで比較的高い精度を出したい
Pythonによる決定木モデル分析方法
決定木モデルは機械学習予測で広く用いられている手法であり、基本的にはYes/Noでこたえられる質問で構成された階層的な判断にて予測を行います。
以下に決定木モデルのメリット/デメリットをまとめます。
メリット
- 単純なアルゴリズムであるため、予測結果にどの説明変数が寄与しているのか簡単に説明ができる
- データのスケールに対して影響を受けない (正規化、標準化は不要)
デメリット
- 過学習を起こしやすい
上記のデメリットである過学習という点に関してもアンサンブル学習やハイパーパラメータの調整行うことで、対策が可能です。
したがって享受できるメリットの方が大きく、実務上も決定木系のアルゴリズムが広く用いられています。
アンサンブル学習とは
アンサンブル学習とは複数の機械学習モデルを組み合わせることで、より強力なモデルを構築する手法。
決定木モデル(Decision Tree)の代表的なアンサンブル学習モデルとしてランダムフォレスト(Random Forest)があげられる。

過学習にさえ注意すれば実用性十分!!
決定木の予測モデル概要
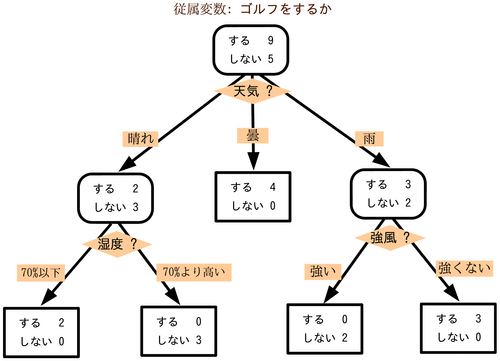
決定木モデルでの予測手法を簡単に可視化したものが以下になります。
この例では「ゴルフをするかしないか」の2分類を予測することを考えます。モデルを構成する訓練データをもとになるべく少ない質問で正しい答えにたどり着くことが目標です。
1つ目の説明変数に天気がある場合、晴れ、雨、曇りそれぞれに関してゴルフをするかしないかを分類します。
晴れの場合、2つ目の説明変数には湿度があるのでその閾値でゴルフをするかしないかを再度分類します。
このような分類を指定した決定木の深度(図の場合は深さ2) まで行うことで最終的な端点でのゴルフをする人数としない人数を比較し、予測モデルを構築します。
考え方自体は単純だね!!

決定木分類(Decision Tree Classifier)のハイパーパラメータ
今回は決定木モデルのうち、分類モデルを扱うDecision Tree Classifierを用います。
Decision Tree Classifierのハイパーパラメータを以下に示します。
詳細に関しては以下の公式リンクを確認ください。
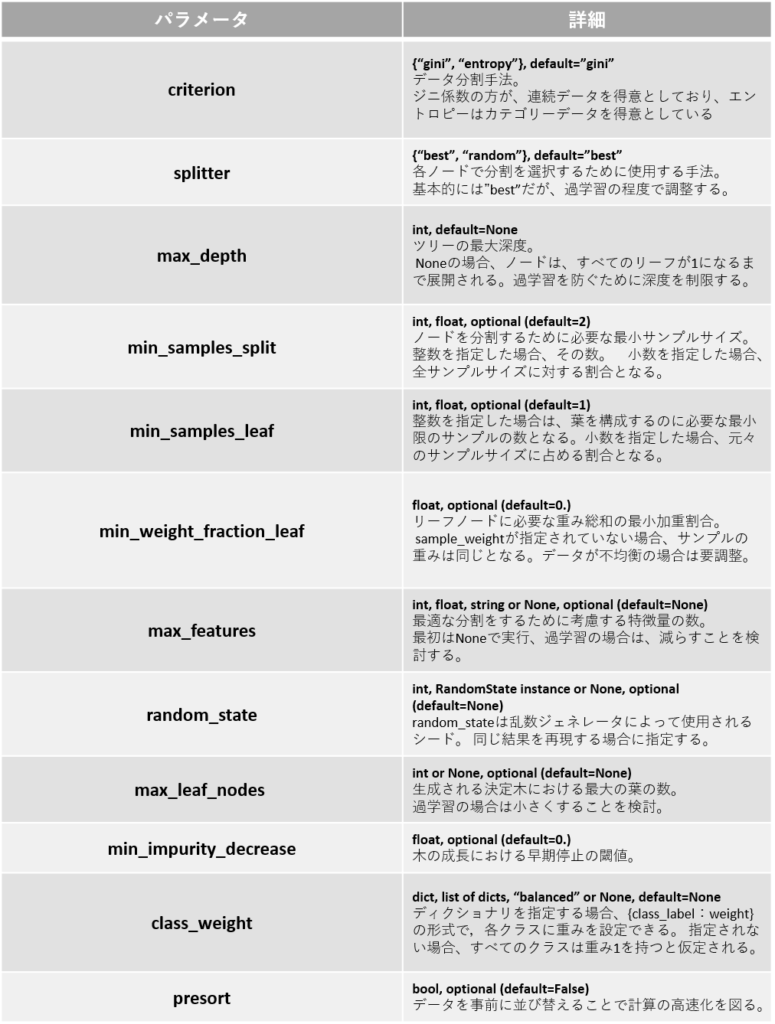

少しパラメータが多くて困るなぁ、ただmax_depthが重要なのは理解OK!
Scikit-Learn Cancer Datasetによる分類モデルの構築
必要なライブラリの読み込み
実際にScikit-LearnのCancer Datasetを用いて分類予測を行います。
まず機械学習予測に必要な必要なライブラリを読み込みます。 "classfication_report"は予測値の評価に用います。
# 必要なライブラリの読み込み
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# 機械学習モデル
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
# 予測値の評価用
from sklearn.metrics import accuracy_score
from sklearn.metrics import classification_report
#sklean cancer dataの読み込み
from sklearn.datasets import load_breast_cancerCancer Datasetの確認
分類のデータサンプルとしてScikit-Learnの提供する乳がんの分類データセットを使用します。
データセットの詳細はこちら↓
以下でデータの詳細を確認しましょう。
dataset = load_breast_cancer()
# 特徴量 (説明変数)
X = pd.DataFrame(dataset.data,
columns=dataset.feature_names)
#ラベル(目的変数)
y = pd.Series(dataset.target, name='y')
# データ詳細確認
print('X shape: (%i,%i)' %X.shape)
print(y.value_counts())
display(X.join(y).head())X shape: (569,30)
1 357
0 212
Name: y, dtype: int64
mean radius mean texture mean perimeter mean area mean smoothness mean compactness mean concavity mean concave points mean symmetry mean fractal dimension radius error texture error perimeter error area error smoothness error compactness error concavity error concave points error symmetry error fractal dimension error worst radius worst texture worst perimeter worst area worst smoothness worst compactness worst concavity worst concave points worst symmetry worst fractal dimension y
0 17.99 10.38 122.80 1001.0 0.11840 0.27760 0.3001 0.14710 0.2419 0.07871 1.0950 0.9053 8.589 153.40 0.006399 0.04904 0.05373 0.01587 0.03003 0.006193 25.38 17.33 184.60 2019.0 0.1622 0.6656 0.7119 0.2654 0.4601 0.11890 0
1 20.57 17.77 132.90 1326.0 0.08474 0.07864 0.0869 0.07017 0.1812 0.05667 0.5435 0.7339 3.398 74.08 0.005225 0.01308 0.01860 0.01340 0.01389 0.003532 24.99 23.41 158.80 1956.0 0.1238 0.1866 0.2416 0.1860 0.2750 0.08902 0
2 19.69 21.25 130.00 1203.0 0.10960 0.15990 0.1974 0.12790 0.2069 0.05999 0.7456 0.7869 4.585 94.03 0.006150 0.04006 0.03832 0.02058 0.02250 0.004571 23.57 25.53 152.50 1709.0 0.1444 0.4245 0.4504 0.2430 0.3613 0.08758 0
3 11.42 20.38 77.58 386.1 0.14250 0.28390 0.2414 0.10520 0.2597 0.09744 0.4956 1.1560 3.445 27.23 0.009110 0.07458 0.05661 0.01867 0.05963 0.009208 14.91 26.50 98.87 567.7 0.2098 0.8663 0.6869 0.2575 0.6638 0.17300 0
4 20.29 14.34 135.10 1297.0 0.10030 0.13280 0.1980 0.10430 0.1809 0.05883 0.7572 0.7813 5.438 94.44 0.011490 0.02461 0.05688 0.01885 0.01756 0.005115 22.54 16.67 152.20 1575.0 0.1374 0.2050 0.4000 0.1625 0.2364 0.07678 0
上記からわかるようにScikit-Learn Cancer Datasetには説明変数(特徴量)が30、569のデータポイントがあります。
目的変数(ラベル)のうち"1"が良性の腫瘍、"0"が悪性の腫瘍を示します。
Decision Tree Classifierによる分類予測 (ハイパーパラメータ調整なし)
次にDecision Tree Classifierを用いてCancerDatasetの分類モデルを構築します。
Scikit-Learnにおけるtrain_test_splitを用いて訓練データとテストデータ用にX_1データを分割します。
今回は訓練データをX_1の80%(569x0.8=455)、テストデータをX_1の20%(569x0.2=114)とします。
まずはハイパーパラメータに関してはrandom stateのみを指定し、その他はdefaultで予測モデルを構築します。
# ホールドアウト
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.20,random_state=0,stratify=y)
Column_List_train = X_train.columns
#ハイパーパラメータの調節は無し
tree = DecisionTreeClassifier(random_state=0)
tree.fit(X_train,y_train)
print("Decision_Tree_Cross-validation train_scores: {:.2f}".format(tree.score(X_train,y_train)))
print("Decision_Tree_Cross-validation test_scores: {:.2f}".format(tree.score(X_test,y_test)))Decision_Tree_Cross-validation train_scores: 1.00
Decision_Tree_Cross-validation test_scores: 0.94
結果からtrain_scoreでのバリデーション予測精度100%となり、モデルが過学習を起こしていることが推測されます。
Decision Tree Classifierによる分類予測 (ハイパーパラメータ調整あり)
次にハイパーパラメータの内、決定木の深度(max_depth)を5に調整して過学習を抑制した結果を以下に示します。
# ホールドアウト
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.20,random_state=0,stratify=y)
Column_List_train = X_train.columns
#ハイパーパラメータの調節は無し
tree = DecisionTreeClassifier(random_state=0,max_depth=5)
tree.fit(X_train,y_train)
print("Decision_Tree_Cross-validation train_scores: {:.2f}".format(tree.score(X_train,y_train)))
print("Decision_Tree_Cross-validation test_scores: {:.2f}".format(tree.score(X_test,y_test)))Decision_Tree_Cross-validation train_scores: 0.99
Decision_Tree_Cross-validation test_scores: 0.95max_depthを5に指定したことで少しばかり過学習が抑制され、テストセットにおける精度も上昇していることが分かります。
十分な汎用性を得るためにはこのようにハイパーパラメータを調整することが必要です。
予測モデルの説明変数 重要度の可視化
決定木系モデルの最も有益な点として予測モデルの精度に寄与している説明変数の重要度を定量化できる点があります。
今回構築したモデルの説明変数の重要度を以下で可視化してみましょう!
feature = tree.feature_importances_
label = X.columns
indices = np.argsort(feature)
# 特徴量の重要度の棒グラフ
fig =plt.figure (figsize = (10,10))
plt.barh(range(len(feature)), feature[indices])
plt.yticks(range(len(feature)), label[indices], fontsize=14)
plt.xticks(fontsize=14)
plt.ylabel("Feature", fontsize=18)
plt.xlabel("Feature Importance", fontsize=18)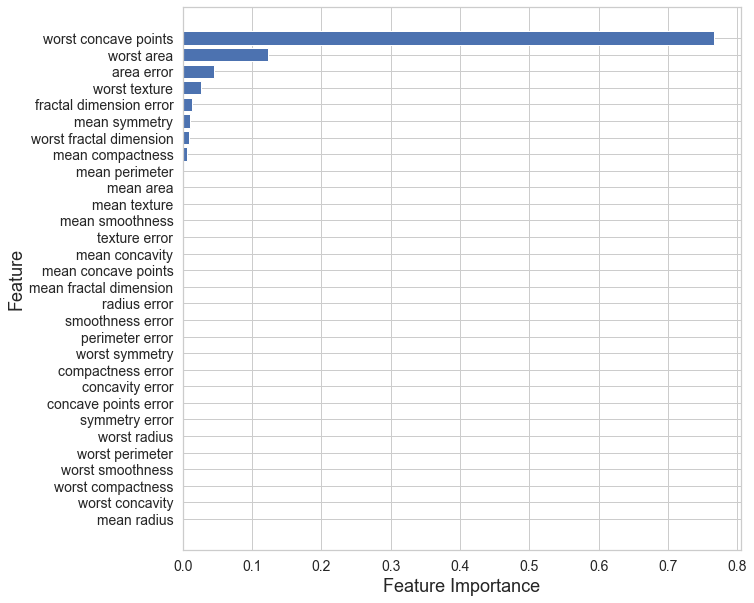
本結果より、乳がんの悪性、良性を判断するにはworst concave points(輪郭の凹部の数の最悪値)が最も重要であることが分かります。
この結果が医師の経験と一致すればモデル自体の有用性にも説明がつくため、実際に実務に活用できる可能性が高まります。
まとめ
今回は決定木モデルの概要とその使用方法に関して具体例とともに紹介しました。
何度も説明しましたが、決定木モデルでは説明変数の重要度を可視化できる点が最大のメリットになります。
実務にて予測モデルの上司への説明や、顧客への説明が必要な場合には決定木系モデルを一番初めに試すのが良いかもしれませんね。
同じCancer Data Setを用いたk-NN法の予測モデルを以下で紹介していますのでこちらも参考にしてください。
また実際にpythonを用いたコーディング学習にはData Campがおススメです!
詳細に関してはこちらで紹介しています。↓
本日は以上です!